得点期待値について

この間、弟と野球を見ている時にふと彼が

「俺はどうも得点期待値というものが信用ならないんだよな。あれってバッターが誰だとか、ピッチャーが誰だとか考えずに、すべての場面の平均得点を出してるんでしょ？でも現実には、打線は1~3番の上位打線のほうが出塁しやすくて、下位打線の方が出塁しにくいんだから、例えばランナー23塁のチャンスも必然的に3~5番の方が、1,2番よりも多く回数があるわけで、それを平均しちゃうってのはどうもしっくりこないんだよなぁ」

というような事を言っていまして、確かに似たような雰囲気のことは僕も思って居たのでちょっと得点期待値について考えていました。

得点期待値の計算方法はとても単純で、野球で起こりうる状態（アウトカウント、ランナーの有無での3*2^3=24通り）の場合それぞれの場面が合った時に、実際の試合でその後何点点数が入ったかを数え上げて、それを起こった回数で割るというものです。

具体的には、ある試合でワンナウトランナー13塁の場面が3回起こって、それぞれその場面の後にホームラン凡退凡退（3点）、ゲッツーで3アウト（0点）、犠牲フライ凡退（1点）となっていれば、ワンナウト13塁の得点期待値は(3+0+1)/3=1.33 となります。

これをシーズンすべての試合で計算したものが得点期待値です。

注意しなくてはいけないのは、これは実際の試合で起こったことを平均しているので、打者や投手のバラ付きが含まれているという点です。

例えば、ノーアウト満塁の場面について考えてみましょう。（ちなみにノーアウト満塁での得点期待値は2013年シーズンでは 2.201 です）
今実際の試合でノーアウト満塁の場面が訪れた時に、「この後平均で2.201点入るから、2点は硬いな」と考える人がいれば、それは微妙に間違っています。（間違っているというよりは、情報をうまく使えていない、と言う言い方が正しいでしょうか。）

何故かと言うと、先の得点期待値2.201というのは、起こったすべての場面での期待であるので、満塁になりやすい投手や打順というのが多く見積もられている、という欠点があるからです。

すなわち、満塁になりやすい打たれまくる投手や打ちまくる打線の影響が大きく、逆に打たれにくく、満塁を抱えない投手や全然打てない打線の影響が小さくなっているわけです。
ですから、「平均的な打者が平均的な投手と対戦した時に、ノーアウト満塁から2.201点入るんだ。」という認識は間違いということになります。

なので、正しく得点期待値を捉えようと思うと、「その場面を作った投手の能力分布がどうなっているかを入手して、今見ている実際の投手＋打者の組み合わせだと、そのなかでどの様な場所に位置しているのかを確認した上で、その後の得点期待値を計算する」という作業が必要になります。

しかし実際には、そのデータを仕入れることも難しいですし、いちいち計算をするのも（普通にテレビで見ている中では）面倒です。
なので、簡易的に考えるとすれば、その時の打者と投手の組み合わせからこれは大方抑えられるな、という場合であれば得点期待値を低めに見積もって、逆ならば高めに見積もるといったことをする、ぐらいが限界でしょうか。

少なくとも、得点期待値を妄信して細かい数字に囚われることは、あまり意味があるとは思えないので、得点期待値はおおまかな傾向と捉えるのが良いと思います。

結局やっているのは条件付き確率の、場合分け変数が連続である場合なのですが、あまり疑わずに使っていると間違った使い方につながるので気をつけないといけませんね。

BaseBall Simulation できました。

作り始めから半年以上経ちましたが、ようやくそれっぽいものが出来ました。

BaseBall Simulation
http://coffeespecial.web.fc2.com/baseballsimulator/index.html

ずーっとC#で頑張ってましたが、C#で作ってもさくっと使えないのが残念なので、Webで動くjavascriptで作ってみました。9回延長戦なしの試合を10000試合行って、その結果を表示します。

選手データを読み込ませる方法をどうやろうか色々考えてる最中で、今はとりあえずすべてrandomにそれなりの選手を6チーム分作ってます。各チームに平均打者と平均投手、それにダルビッシュと二軍選手を混ぜてるので、ピッチャーをダルビッシュにしたらどのぐらい点数が入らなくなるか、とかやってみると面白いかもしれません。

アルゴリズムとしては、ボールに当たる、三振する、ホームランを打つ、の各OddsRatioを打者投手で計算して、起こり易さをOddsとして求めてから確率に変換するという方法を取ってます。なので投手を平均投手にすれば、打者の元能力と同じような打率、出塁率になるようになっています。

javascriptは、以前勉強しようと思った時に、あの適当な型の扱いと呪文のような

(function(x){});

が良くわからなくて挫折していたのですが、C#っぽく静的に型をつけれて、尚且つVisualStudioの補完機能を使えるTypeScriptというjavascriptのコードをコンパイルしてくれるやつを使ってなんとかかんとか再チャレンジしました。

TypeScriptはクラス、インターフェースとかもろもろのオブジェクト指向的な記述をC#と似たような形で導入できるので、プロトタイプチェーンとはなにもんじゃ、クラスがないとは何事だ！死ね！ という人にも扱いやすいんじゃないかなと思います。

実際ぼくもこれを使って、javascriptじゃないみたいにjavascriptを書いていくうちに、だんだんとjavascriptの雰囲気というか、どうやって書けば良いのかをコンパイル後のjsファイルを読んだりしてみて、手を動かしながら理解できてきた気がします。しっかりjsを使いこなすためには一度はちゃんと言語仕様について勉強しないとだめなのもたしかなのですが、そればっかり先行して、まったくやる気がでないよりは、それっぽいものを書いてそれっぽく動いてくれたほうがやる気も出る（気がする）ので、オススメです。やっぱり慣れてない言語を扱うときに、IDEの補完機能があるないは全然書くスピードが違いますね。

あと、何気でVisualStudioWebのhtmlとcssの編集も、かなーり優秀で良いです。4,5年前に初めてhtmlに触った時にこれを使いたかったなって凄い思いました。やっぱり補完機能って神。

中日広島18回戦 盛大なるネタ試合

今日の試合はとんでもなく凄い試合でした．
間違いなくシーズンでもまれに見るネタ試合です．

	1	2	3	4	5	6	7	8	9	10	11	計	安	失
広島	0	2	0	0	0	0	0	0	0	1	3	6	9	1
中日	0	0	0	0	0	0	1	1	0	1	2	5	14	1

戦評 8月29日(金)中日 vs. 広島 18回戦

広島が熱戦を制した。広島は2-2で迎えた延長10回表、松山の適時打で勝ち越す。直後に同点とされるも11回、田中の適時打などで3点を挙げ、勝ち越しに成功した。5番手で登板したミコライオが今季初勝利。敗れた中日は、終盤に粘りを見せるもあと一歩及ばなかった。
http://baseball.yahoo.co.jp/npb/game/2014082902/top

ぱっと見平凡なただの延長戦ですが内容がすさまじい

まず皮切りは7回裏の小笠原のタイムリー．思い出してますね．

その後の赤松の守備もまたすごい．

赤松はその後得点にはつながらなかったものの9回に連続盗塁も決めてます．
流石守備走塁でプロやってるだけあるな（失礼）．

そしてあれよあれよと9回になり，同点で登板したのは防御率5点間近の中崎．そしてルナ森野に連続ヒットを許しノーアウト12塁の大ピンチ． 僕は完全に負けを覚悟してこの時点で見るのをやめました．しかしこの後謎の神ピッチを見せて0点に抑えました．いーやよくやったよ中崎期待してなくてごめんね.

お次は10回表，代打の天谷がスリーベースをうち，その後タイムリーが出て1点．こうなれば今年安定感抜群のミコライオが締めて終わりとおもいきや，まさかの失点で同点に．

更に11回，丸梵のヒットでワンアウト13塁のチャンスを作ると，代打赤松が広島お家芸スクイズ． がしかしピッチャー正面に転がり3塁ランナー丸は余裕でアウトのタイミングで万事休す，かとおもいきや何故かピッチャー小川が焦ったのか近距離で谷繁にトスして谷繁は取れず，オールセーフでノーアウトランナー2,3塁に．続く田中もスクイズの構えでまたしても焦ったかパスボール．赤松は3塁まで到達．結果として何もせず2点を取りました．どことなく一昨年の松山の悲劇を彷彿とさせます．

このあとしれっと田中がタイムリーを放ち一挙3点．

こうなるともう余裕だろ，となるところでカープの抑えは永川．

そんでこの永川が藤井にランナー一塁から今日2本目のホームランを浴びて1点差．しかしその後はなんとか踏ん張りカープが辛勝し，2点取られた永川にセーブがつき，セーブ失敗したミコライオに勝ちがつきました．頑張った大瀬良くん可哀想…

ありとあらゆるネタを詰め込んだような試合で，今日の観に行ってた人は相当面白かったと思います，気が気じゃないでしょうが．

Point Distributionから見る今年の広島東洋カープ

総得点から勝率予想をすることは，セイバーメトリクスの世界では良く行われていることではあります．有名なところでは，ピタゴラス勝率と呼ばれているもので，得点数$a$,失点数$b$とした時に，チームの勝率Pが $$P=\frac{a}{\sqrt{a^2+b^2}}$$ であたえられるというものです．こんな簡単な式ですが案外うまくフィッティングするのでよく用いられているのですが，理論的な考察としてなぜこの式が有効なのかという議論をしているものはあまり見たことがありません．おそらく，野球の得点が入るという現象がrandomの結果として考察しづらいことが要因ではないかと考えています．
野球において得点が入る，とはどういうことかを考えてみます．当たり前ですが，点が入るということは3アウトになるまでにランナーが本塁まで進塁するというふうに考えることが出来ます．なので，ヒットが3本続いたとしても点が入らない場合もある一方で，本塁打が出れば確実に点が入り，また安打が一つの回に固まると，本塁打以上の大量得点が得られます．なので，打撃結果と得点が単純な比例ではありません．
実際，サッカーの得点や野球の一試合あたりの本塁打数の分布はポアソン分布に従いますが，野球の得点はポアソン分布よりも，高得点側の確率が高い分布になってる気がします．

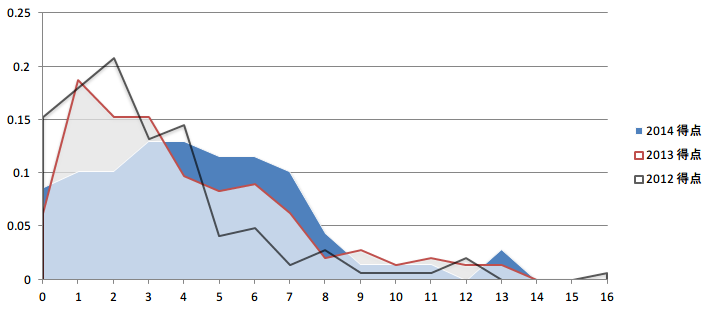
Point Distribution (＠2013 横浜ベイスターズ)

2013年カープの得点分布でも，ポアソン分布のピークがなだらかになり，高得点側に推移したような形となっています．他のチームに関してもまあ概ねこのような分布になっているので，得点がポアソン分布に従うということを仮定するのはマズイかなといえると思います．

で，やりたいのは今年去年よりだいぶ健闘しているカープの得点分布が去年と比べてどうなっているのか見てみましょうということです．結果は以下の様な感じ

Point Distribution(@広島東洋カープ 2012~2014)

縦軸は得点確率，横軸は得点数

去年と比べて低得点の割合が減少していることがわかります．まあそもそも平均得点が3.8→4.3になってるので右に寄ることは当たり前なのですが，得点分布自体が全体通して均一になっています．やっぱり今年奮起してるエルドレッドの長打（本塁打）のお陰で，得点が安定して取れるようになっているからなのかはたまた別の理由からなのか．失点分布はそれほど変わってない様子なので，安定して4,5点取るっていうのは勝率アップにつながるのかも．

チームの長打率とか出塁率とかとリンクさせて分布傾向を出したりすると，同じ平均得点のチームでも，強い弱いの評価が出来て面白そうっすね．

ちなみに巨人はこんな感じ どっかで今年の巨人はOPS.750~.800の打者ばかりで圧倒的に打てる打者がいないというのを見ましたが，そのせいで高得点側の確率が上がって，6,7点あたりの確率が低い事につながってるのかも．

数列の収束における有界単調数列の使い方

$$ a_{n+1}>a_n, a_n>1 \Rightarrow {a_n} は下に有界な単調数列 $$

定理：有界単調数列は収束する 単調増加で，上に有界な数列${a_n}$が集合$A=\left\{a_1,a_2,......\right\} $の上限$\alpha$に収束することを示せば良い. $\forall\varepsilon>0$に対して$\alpha-\varepsilon$は$A$の上界ではない. $${n>N_0 \Rightarrow \alpha-\varepsilon<{a_n}<\alphaなるn_0が存在する}$$ このとき $$|a_n-\alpha|<\varepsilon$$ であるから，a_n$rightarrow\alpha$が示された．

C#でWebからデータを取ってくる

C#でwebからデータを取ってくるってことはあまり考えたことがなかったのですが、ちょっとプロ野球の得点分布を知りたいなと思った時に、いちいちデータを手打ちで集めるのも面倒だから自動化出来ないかなぁと考えて色々さがしてみたところ、C#でもhtmlのDOMを自在に操れるHtmlAgilityPackなるものがあるらしいのでちょっとテスト。

使い方としてはまず using System.Net でネットワーク関連のusingをもって来ておいて、HttpWebRequestとHttpWebResponseでデータを読み込みます。この時にもっと単純に取ってくるWebClientというクラスもあるのですが、それよりもrequestとresponseでストリーミングで読み込んだほうがUI（フォーム表示用）スレッドと読み込みスレッドを分離できるので、読み込み時にフォームが固まることを防げるのでよいらしいです。

WebClientよりHttpWebRequestを使った方がいい理由
http://d.hatena.ne.jp/kabakiyo/20120224/1330066622

あとはその読み込んだstringをHtmlAgilityPackにほり込んで、SelectNodesでjQuery的に検索してやれば勝手にほしいとこだけを検索して出してくれるという流れです。とってもシンプルでいいですね。

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.IO;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.Net;

namespace web
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        string baseurl = "http://baseball.yahoo.co.jp/npb/game/";

        private void button1_Click(object sender, EventArgs e)
        {
            DateTime dt_now = DateTime.Now;
            string date = dt_now.ToShortDateString().Replace("/", "");

            // 今日の試合を読み込むためにurlを加工
            string url = baseurl + date + "01" + "/stats";
            //ex).url = http://baseball.yahoo.co.jp/npb/game/2014052801/stats

            HttpWebRequest req = (HttpWebRequest)WebRequest.Create(url);
            req.Method = "GET";
            HttpWebResponse res = (HttpWebResponse)req.GetResponse();
            Stream s = res.GetResponseStream();
            StreamReader sr = new StreamReader(s);
            string context = sr.ReadToEnd();
            HtmlAgilityPack.HtmlDocument doc = new HtmlAgilityPack.HtmlDocument();
            doc.LoadHtml(context);

            HtmlAgilityPack.HtmlNodeCollection _nodes = doc.DocumentNode.SelectNodes("/html[1]/body[1]/table[1]/tr");
            if (_nodes == null)
                break;
            foreach (var node in _nodes)
            {
                textBox1.Text += node.InnerText + "\r\n";
            }
        }
    }
}

久しぶりに

めっちゃ前に作ってた野球シミュレータの改良をやりました。

たまにはいじらないと自分で書いたコードが暗号に見えるようになりますね。すでに意味不明部分多数で手遅れ感満載ですが。

ほんとうはjavascriptかなにかweb上で動くもので作れればいろんな人に使ってもらえる可能性も増えて、いろいろと改良する点も意見としてもらえると思うのですがいかんせんC#しか使えないということと今現在新しい言語をいじくる余裕があまりないというので停滞中です。一応javascriptの本とか買ったんですけどね。ほとんど手付かず状態です。

とはいっても、C#でうまく設計さえできれば他の言語でかくのも結構楽にできるんではないかと（勝手に）予想してるので当分の目標はC#のWindowsWPFアプリケーションとして仕上げたいなぁともくろんでます。今のところ新しいやつでは

• DHありなしの対戦
• CSVで登録する選手を任意に決定できる
• 先発ローテーション（最終的には抑えの登板とかも）実装
• 天候、パークファクターの導入（まあこれは別にいいっちゃいいかな）

といった当たりをできるようにすることを目標にしてます。さっき見返してたら地味にもうこれ作り始めてから半年以上経ってるんですよねこれ。完成するのいつかな…

セイバーメトリクスな数字

打率、ホームラン、打点、勝ち星、得点圏打率というよく見る数字に比べて、出塁率や長打率、あるいはOPS(ここらへんは割りと浸透してるのかな？）,XR,Fip,Dip,IsoD,IsoP,LOB%……とかいったセイバーメトリクス的な数字は市民権をまだまだ得れていない感じがあります。人によってはセイバーメトリクスの数字は実際の試合を見ていない数学オタクがでっち上げたもんでそんなのには意味が無いとかいう人もいたり。

じゃあそもそも、打率ってそんなに自然な数字なの？という話がでてきます。何気なく使っている打率ですが、あれの計算方法も全ての安打を無差別に足し算するという作業をしていますから、当然恣意的な指標です。しかもフォアボールはカウントされませんから、フォアボールを選ぶことは打率を上げると言う観点からいうと全く無意味です。ですから打率だけで打者の能力を図ろうとするときには、そういった消えた要素があることを考えていないと、間違った結論を導く可能性があります。

たとえば、ノースリーから毎回打ちに行ってフォアボールは選ばないし打っても毎回単打の3割バッターと、打てばほとんどホームラン、フォアボールも選びまくる3割バッター、この二人が同じになってしまうのが打率です。ここまで酷いことは無いと思いますが、そのような可能性があることは頭の何処かに考えて置く必要があります。

打点とか勝ち星とかいったものに関してはもっと不条理で、ヒットは打つものの毎回運悪くランナー無しで回ってくる弱小チームの四番よりも、周りが打ちまくるせいで毎回ランナーがいる状態で回ってくる打者の方が明らかに有利ですし、勝ち星なんてのは自分が打たれまくっても打線がバカバカ打てば増えるし、去年のいつかのDeNAの高崎投手みたいに、自責点0失点2で尚且つ自分がヒットを打って1点とって8回まで投げたとしても打線が打てずに負けてしまえば負けになるというある意味論理的でない無茶苦茶な数字です。

このように、指標の妥当性という面からセイバーメトリクスな数字を批判するのは無理があります。結局は、打率とOPSなにがちがうのかっていうのは、見慣れているのかそうではないのか、ただその違いに尽きると思います。

例えば今一般によく用いられる指標としてセーブとかHP（ホールドポイント）がありますが、あれはつい最近まで日本球界には存在しませんでした。しかし先発完投型の試合構成であったのが、先発→中継ぎ→抑えという分業制へと移行していく段階で、途中で登板する投手の地位向上が図られ、中継ぎを評価する指標として導入されたのがセーブといった概念です。では、セーブが無い時代の抑えで活躍した選手に価値がないかというとそんなことは無いですよね。今の時代の人と同じようにチームの勝利に貢献しているはずですから、同じように評価されるべきです。しかし、その選手がいた当時にはそんな概念がありませんから、おそらくは先発投手に比べてかなり選手としての価値が低いとみなされていたでしょう。

このセーブやホールドポイントと同じように、今一般に普及している指標だけが万能で十分である、とは必ずしも言い切れないはずです。そのためいろいろな側面から選手を見てやる方法として、セイバーメトリクスがあるんだと思っています。打者指標のIsoDを見れば、どれだけフォアボールを選ぶ傾向があるバッターであるかが、投手指標の一つであるFipを見れば、守備の影響から独立してどの程度その投手が抑えることが出来るのかといったことをある程度客観的に判断できます。

従来指標が絶対だ！という立場を頑なに守ろうとすると、結果として現実を見ることができなくなる恐ろしさがあります。

この記事は http://www.fangraphs.com/blogs/a-response-to-bob-ryan/を読んで思ったことをつらつら書いた（というか多分に影響を受けてい書いた）のですが、あらためて物事を認知する難しさや主観の危うさを感じれた気がします。

さきほどの内容も、セイバーメトリクスの指標を使う時にそれが絶対だという立場にたてば結局おなじことになるわけで、そこは常に注意して行かないといけないところです。

I think telling an accurate story is more important than telling a comfortable one, and the reality is that the numbers that are commonly used generate stories that are factually incorrect. ........
We’re not replacing the “Holy Trinity” of baseball statistics because we can’t enjoy the game. We’re pointing out that these statistics breed false narratives, and we value the truth.
A Response to Bob Ryan http://www.fangraphs.com/blogs/a-response-to-bob-ryan/

ランナー二塁でのチームバッティング

今日の巨人対ヤクルト戦、5回ノーアウトランナー二塁、バッター比屋根の場面。このような場面で間違いなく実況が言うのが、「バッターは最低でもファーストもしくはセカンドゴロを打てるように流し打ちを心がけて欲しいですね」というコメントです。今日も解説の江川がそのようなことを話していました。

確かにライト方向へのゴロならば２塁ランナーはサードへ進めますし、もしサードやショートへの強烈な当たりであればランナーは動けず流れが悪くなるというのも一理あります。

しかし、当然それを見越してピッチャーも左バッターならばアウトコースへのストレート、右打者へならインコースへのチェンジアップなどを軸に流し打ちをさせない投球をしてくるでしょう。そのような流し打ちをしてヒットを打つことが難しい場面において、監督は無理に流し打ちを意識させる必要があるのでしょうか。

まず、ノーアウトランナー二塁と言う状況では平均的にどの程度の点数を得ることが出来るのかを確認します。以下の表は2013年のNPB全試合においてノーアウトランナー二塁の状況が発生した後得られた点数の平均値を表しています。

situation	アウトカウント	得点期待値
2	0	1.022

これを見るとノーアウトランナー二塁は平均的に見れば1点取ったことと同義であると言えます。では次にこの状況から起こりうる状況変化を考えます。

ノーアウトランナー二塁で起こりうるものとして、四死球、シングルヒット、ツーベース、スリーベース、フライもしくは2,3塁へのゴロアウト、1,2塁へのゴロがありますが、今回は簡単のためスリーベースとホームランは考えないこととします。

バッターの結果による次の状況の得点期待値が次の表です

situation	アウトカウント	得点期待値	差分
2	1	0.713	-0.309
3	1	0.873	-0.149
1-2	0	1.41	0.388
1-3	0	1.736	0.714

これを見ると思ったより1アウトランナー3塁の得点期待値がよろしくないです。ノーアウト2塁時よりも得点期待値はだいたい0.15点ほど減少します。当然1アウトランナー2塁のほうが低いのですが、くらべても0.2点以下の差しかありません。

一方もし打者がヒット、もしくはフォアボールを選べば得点期待値はぐっと上がります。フォアボールでも0.4点、ヒットなら0.7点分の価値です。ここには載せていませんが、ノーアウトランナー1塁での得点期待値が0.44であることを考えると、このシチュエーションでヒットを一本追加することは、ノーアウトでランナー無しの時に単打もしくはフォアボールを選ぶときに得られる得点期待値よりも1.7倍ほどの価値があることがわかります。

しかも、ランナー二塁で強打が成功しツーベースを放てば、1点獲得した上にその後の得点期待値は1.022のままですし、ホームランを打つ可能性も当然含まれますから、強打策は更に大きな得点寄与となることが予想できます。

以上のことから、長打が見込まれるバッターや、ライト方向への打球を打とうとすると打率や長打率の下がってしまう選手は、普通に打たせるべきだということが言えるでしょう。

今日の試合の場面ではバッターは比屋根ですから、長打は少ないし次の川端バレンティンで点を取れば良いと考えて右打ちを指示することは、それほど間違った選択ではないですし、むしろセオリー通りです。

しかし続く打者が川端、バレンティン、雄平ということは、裏を返せば打撃能力が高く大量得点が見込める場面であるとも言えます。また比屋根は右打者で、尚且つ今シーズン3割近い打率を誇り、打球方向は主に左に寄っています（http://baseballdata.jp/playerB/1100052.htmlによると33打席中ライトへ飛んだ打球はわずか4球です）から、比屋根はそこまで右打ちが得意であるようには見受けられません。したがって、右打ちを指示した時の打率が下がってしまう可能性は十分考えられます。

加えてヤクルトは現在救援陣の防御率が極端に悪く3点差程度であれば試合後半にひっくり返されてしまうというリクスがあります。以上のことを鑑みると、確実に1点を取るよりも強打で大量点を取ってトドメを指すという指示もありではないのか、と思ったりもします。

本を買いました

一冊280円という安さにつられてついつい買ってしまいました。技術系の本を読んでると、一冊1000円ぐらいまで安く感じてしまうのは病気だと思います。

今回もまたAmazonで。立ち読みしなくても欲しいなと思う本は殆どAmazonかもしくはhontoで買うようになりました。

特にhontoは定期的に200円～500円offのクーポンを配ってくれるので貧乏学生にはとても助かります。まわしもんではないですが結構オススメです。欠点は発送がちょっと遅いことですかね。

与謝野晶子とか読んだこと一切なかったのでちょっとチャレンジですね。青空文庫でざっと見た感じ古文の授業を受けてないに等しい僕には厳しい気もしますが頑張ります。

異なるリーグに所属する選手同士の対戦予測

今回は異なるリーグに所属する選手同士が、あるリーグで対戦した時にどの程度の成績を残すのかということを考えてみたいと思います。今まで考えていたのはおなじリーグ内部での話でしたから、最終的に少しリーグ平均のOddsでいじれば良かったのですが、投手打者そして今現在所属するリーグが異なっている場合ちょっとややこしくなります。

具体的には打者が打高のリーグに所属投手が投高のリーグに所属そして現在のリーグの反発係数が2つのリーグに比べて高いというような場合です。 ボールが飛びやすかったり、球場が狭かったりと言った平均的に打者が有利なリーグに所属している場合は、打者および投手の安打発生Oddsは高くなる傾向にあります。逆の場合も同様で、したがって異なるリーグに所属している選手同士を対戦させようとする時は、それぞれが所属するリーグの影響をまず取り除き、その上でodds ratioを考えるのが妥当でしょう。

Oddsを用いる成績予測の考えの根底には、選手の突出度をOdds同士の比であるOdds Ratioによって比較するという概念があります。この作業は、数学や物理でいうところの規格化手法です。規格化とは、ある値を基準として、自分の大きさをそれの何倍かで表すという考えです。これを考えれば、打者、投手、今考えているリーグをLb,Lp,Lthisとすると $${Odds Ratio}_b=\frac{Odds_b}{Odds_{Lb}}$$ $${Odds Ratio}_p=\frac{Odds_p}{Odds_{Lp}}$$

という風に表せます。これを掛け算することで、打者と投手を合わせた突出度を計算できます。そしてそれに今打者と投手が所属するリーグのOddsを掛け算することで、今いるリーグの平均と比べることができ、合理的にOdds Ratioを算出出来ます。 $$Odds Ratio_{AvsBonLthis}= Odds Ratio_b\cdot Odds Ratio_p\cdot Odds_{Lthis} $$

• $Odds Ratio_{AvsVLthis}$ : AとBがリーグLで対戦した時のオッズ
• $Odds Ratio_b$ : Batterのオッズ比、リーグでの卓越度
• $Odds Ratio_p$ : Pitcherのオッズ比、リーグでの卓越度
• $Odds_{Lthis}$ : PitcherとBatterが所属するリーグのオッズ

ex).平均打率0.300のリーグで0.350打つバッターと平均打率0.270のリーグで被打率0.280のピッチャーが超低反発球が導入された平均打率0.220のリーグに所属する場合の期待される打率 $$ \begin{aligned} Odds Ratio_{Lthis} &=\frac{0.350/(1-0.350)}{0.30/(1-0.30)}\cdot \frac{0.28/1-0/28)}{0.27/1-0.27}\cdot 0.220/(1-0.220)\\ &= 0.372\\ &\therefore P = \frac{0.372}{1-0.372} = 0.271 \end{aligned} $$

しかしこの考え方にも欠点があります。それは、比べるリーグのレベルが明らかに異なる場合です。

例えば少年野球チームで平均以上にヒットを打つバッターと、プロ野球選手だけど1軍ではボコボコに打たれまくった投手が対戦するときなどにはこの方法を用いてはいけません。Oddsの考え方の基礎にあるのは、その選手が平均値からどれだけ突出した選手なのか、ということに焦点を合わせて結果を推定するというものです。

そのため、比べる2選手の所属するリーグの選手の能力が基本的にはほとんどおなじであるということが大前提となっています。したがって、同一のリーグでも大きく年代が異なる選手同士の対戦成績予測や、NBPとMLBといった明らかに能力の平均値が異なるリーグの選手同士の成績予測にはこの方法を用いるのは適切ではありません。

複数の可能性がある確率でのOddsRatioの使い方

前回に引き続いて、OddsRatioのお話

OddsRatioが勝率の違うチーム同士の対戦成績や、ある打者と投手が対戦した時の打率や奪三振がどの程度の確率で起こるのかを計算する際にとても有効であることについて書きました。

今回考えて見たいのは、確率の分岐先が複数存在する場合です。

野球シミューレーションを作る時に大事なこと

FanGraph今月のまとめ!みたいな記事に乗ってた、シミュレータを作る上で学んだ10のこととかいう最近ネットでありがちなタイトルの記事がなかなかおもしろいことを書いてあったので、ちょっとメモ

野球における打率とサイコロ

去年あたりから、プログラムの練習を兼ねて野球のシミュレータを作っています。
その時改めて野球の結果と偶然とか確率と言ったことについて考えた時に、ふと疑問に思ったことがいくつかあったので、この間Twitterでどばどばと適当に垂れ流した内容をもとにちょっと考えを練りなおしてみました。

1.打者の結果はサイコロとおなじなのか？

例えば出塁率.400のバッターが居たとして、そのバッターが10打席回ってきた時にヒットを打つ本数と、仮に10面あるサイコロが合ったとして（このような過程は乱数を用いれば作ることが可能です）、そのサイコロのうち1~4の面が出れば出塁とする場合とで厳密に言うとヒットの出方が違うのではないか、と言う疑問です。

ちょっとややこしいのですが、野球における打率や出塁率などの率系の指標はあくまで得られた平均値でしかなく、平均的にサイコロとおなじ割合でヒットが出るとしても、そのばらつきまでもおなじであるとするのには、大雑把には近似できるとしても厳密には異なるのではないかということです。
サイコロであれば、その時の出塁の数は二項分布で表現できます。一方現実の野球選手の出塁が決まる過程は、ピッチャーが投げた球がストライクになるかどうかとか、打った球がどこに飛んで行くかとか言ったもっと上位の過程の結果として表されるので、最も確率が高いのはサイコロで表した際の最尤値と一致するとしても、そのまわりの値を取る確率が先の二項分布で表される確率とくらべて高い、もしくは低い可能性は捨て切れません。

図１：N=50,p=0.30の二項分布（青色）と予想した現実の分布の違いのイメージ図。縦軸は確率。

とまあそんなことを考えていたんですが、いろいろと考えた結果これは間違いであるという結論に至りました。結論をいうと

もし図のような確率分布となるとすれば、おなじヒットを打つ能力を持つ打者が二人板として、序盤の打席でたまたまヒットを多く打った選手はもう一人の選手と比べて、その後ヒットを打つ能力が下がる必要がある。ということです。

普通に考えて、おなじ能力の選手が二人いればその二人が現在立っている打席でヒットを打つ確率は全く同じであると考えられます。したがって1打席だけの結果に注目するとその確立はベルヌーイ試行として表すことが出来ます。ベルヌーイ過程とは、コインを一枚投げた時に表が出ると1,裏が出ると０とみなす実験を行うことを意味します。そしてこのベルヌーイ過程がN回行われた時、出た表の数の合計を確率として表すと二項分布となることは証明されています。したがってこれを逆に考えれば、結果が二項分布とならない過程では、一回一回の打席の結果はベルヌーイ過程ではない他の過程によって決定されている事になります。

これは、過程が行われている時にバッターの持つ平均的な出塁割合 :p の値が変わらないということに矛盾するため、打席が増えるに連れて、過去の打席の結果により現在の打席のヒットを打つ能力が上がる、もしくは下がる事となり、これは直感に反します。
（ヒットを打ったからと言って次の打席は打てないだろうというのは、パチンコで負けたからと言って次の日勝てる確率が上がるわけではないことと同じですね）

ちょっとややこしいのは、この議論では、打者が仮に確定された真の実力pの確率でヒットを打てる、ということを仮定していますが、このpの値は必ずしも打率の値ではない（かもしれない）ということです。

ココらへんはベイズの定理が関連するので、どこまで考えるんぞという話であるうえに私自身しっかり理解できていない可能性が高いので微妙ではあるのですが、プロ野球の打者が持つと期待される打率の値は（恐らく）ある値p'を平均とした正規分布のような確率密度関数で表示できるとします。
次に今シーズンである打率pを残した選手が居たとして、その選手が持つであろう実力の打率qを推定することを考えます。

実際の打席に立つと、実際の過程をへることによるぶれが生じてしまうので、pからのずれが生じます。

これは表と裏が出る確率が1/2,1/2のコインを４回振っても毎回２枚が表になるとは限らないことと同じです。

普通に考えると真の打率はpであるとすればよい様に思うかもしれませんが、例えばpが極端な値.500をとった時のことを考えてみます。これは特に打数の少ない選手で起こりがちですが、たまたま数打席ヒットが多く出たからといって、その選手がイチローを超える打率を真の実力として持っているとは考えれない、せいぜい.300ぐらいであろうとかんがえると思います（普通は）。この作業が先のベイズの定理に当たる部分です。

ほとんどの選手は.250~.280ぐらいの間に真の実力があるとかんがえられますから、そもそも.500の実力を持つ選手は殆どいません。したがって、.500をシーズンの記録として残した選手のほとんどは.250~.280の平凡な実力を持った選手がたまたま運良くヒットが多く出た、と考えられます。これを数学的に調べようと思うと、選手がある真の実力を取る確率に、その実力を持ってシーズンを過ごした際に打率.500を取る確率を掛け算することで調べることが出来ます。これがベイズ的な打率へのアプローチです。

したがってシミュレータを作る際も、来シーズンの予想をするシミュレータをつくろうとするならば、このベイズから推定されたXを用いる方が信頼度が上がるのではないかと考えられます。

とはいえそのような処理をすると、例えば.350で首位打者を取ったようなバッターは「たまたま今シーズンは実力以上のちからが発揮されただけで、本当の実力は平均にもっと近い値に違いない」と推定されて平均へと回帰する圧力がかかりますから、全員の能力が平均化されシーズン予測の値も全チーム似たような得点となる可能性があるので、エクストリームな値が得られない分インパクトとしては小さいものになってしまうかもしれません。

円グラフの話

円グラフってのは全体の割合を角度で表して表示するグラフです。テレビのニュースとかビジネスとかでよく使われてるのを見かけると思うのですが、あんまり使うのよくないらしいという話が書かれた記事を見つけたのでしらべてみました。

Wikipedia 円グラフ
統計学者は、円グラフを情報伝達能力が低いとする傾向がある。円グラフはビジネスや報道ではよく使われるが、科学分野ではあまり使われない。理由の1つは、棒グラフなどに比べて個々の領域の大きさを比較するのが難しいためである。スティーブンスの冪法則によると、面積は0.7乗で知覚され、長さは1.0乗で知覚される。これは、知覚される差異と実際の差異が同じである長さの方が、尺度としては優れていることを示唆している。

 スティーブンスのべき乗則というのは実際のものの大きさの比に対して人間が感じる大きさの比で、要は今回の例だと面積が2倍になっても人間が感じる大きさは2^0.7倍になってる風にしか見えないってことです。長さの二乗が面積になってることを考えると0.7は1/√2におおよそ等しいことからも人間は面積ではなくて長さでものごと判断してるってことが言えるかもしれません。

てなわけで、面積が比例するように作られた円グラフはこの時点で精度という面でかなり使えないことがわかります。しかも世の中には3D円グラフっていうのも存在して、まあ上のことを考えると今度は３乗で効いてくるわけですからもっともっと見た目と実際の量とのギャップは大きくなります。

3D円グラフを使うのはやめよう　http://oku.edu.mie-u.ac.jp/~okumura/blog/node/2266

統計用プログラムRのHelp:Pie
Pie charts are a very bad way of displaying information. The eye is good at judging linear measures and bad at judging relative areas. A bar chart or dot chart is a preferable way of displaying this type of data.

正しい情報を正しく表示するっていう意味合いでは完全に悪者扱いですね。意図なく惰性で円グラフを書くのは危険ってことがわかります。 特にねつ造したいとかそういう意図がなければ棒グラフで書くのが無難です。特に項目ごとの数値を表してるグラフ（さっきの教科書の例みたいなやつ）なら棒グラフで代用できます。というか棒グラフにしましょう。 こういうことって言われてみるとあたりまえなんですけど、実際見た瞬間に円グラフだからこのグラフ作成者はここを強調したいんだな、なんて考えられるかといわれると正直微妙なので、円グラフを見るときには気を付けてみる必要があります。
例として、wikipediaにあった酷い例を挙げておきます。

http://junkcharts.typepad.com/junk_charts/2009/08/community-outreach.html

こういう不思議なグラフを作ることができてしまうので、区切りを恣意的に決められるので適切ではないという例としてよくとり挙げられるヒストグラムよりもさらに悪いといえるかもしれません。あとはこんな例とか

「錯覚立体円グラフに(さらに)データ配置マジック」が混ぜられた「Appleが見せたiPadシェア」　http://www.hirax.net/diaryweb/2012/09/16.html

なかなかにエクストリームですね。ここまで来るとAppleを褒めたくなります。
こうやって調べてみると、学者は円グラフを使わずにマスコミとかビジネスマンが円グラフをよく使う理由がわかりますね。悪い人にだまされないように気を付けないといけません。

NHKの棒グラフ描画システムが機械的に世論を狂わせている可能性　http://takagi-hiromitsu.jp/diary/20070204.html

高校の物理の話

今やってるバイト先では高校の物理を教える機会もあって、今日は物理が嫌いではないけど苦手にしている高2の少年の担当でした。範囲は熱力学。

どうも熱力学第一法則の意味はわかるんだけどその使い方がよくわからないみたいで、もちろん僕も頑張って説明はするんだけどやっぱり教えるのとわかってるのとでは意味が全然違うし、どう考えても僕は教えるプロではないし言い訳をすればきりがないんですが、まあうまいこと伝えることができないわけです。

でもその生徒は数式がわからなくても頑張って食いついてくれるんです、そんでたとえば熱効率の問題で熱機関のエネルギー効率を求めなさい、っていう問題の答え合わせの時にちらっとエアコンの効率は100%を超える理由を言ったときとかにすごくいい顔をするんです。あとは跳ね返り係数を求める問題で、高さの比だけで係数が出せるとか、そういったちょっとした物理のtips?みたいなものが出てきたときですね。物事を俯瞰した視点から見れるっていう面白さはわかってくれてるんです。

日頃何気なく見てる現象とかが自分の知ってる知識で説明できる喜びっていうのはやっぱりみんな持ってて、それをもっと教えてあげる場面を学校でつくるってあげればもっと物理とか数学とか科学とかが好きになる子が増えるんじゃないかなと改めて思ったわけです。

確かにボールを投げ上げた時の高さと初速の関係とかは大事なんですけど、その式だけを闇雲に暗記させてこの問題はこう説くんだ！って教えてテストでぎりぎり合格点をとってきてあとは知らんっていうのもちょっと寂しいなと。

とはいっても毎回毎回わかりやすい身近な例を出してくるのも大変だし、勉強って最初はわからないものをうのみにする技術も（すくなくとも答えのある勉強に関しては）なかなか有効で、一概にそれをやめろとも言い難いのも事実で、どうやってその配分をとればいいのかなぁと考えてしまいます。もんもん。